Logarithms
We’ve encountered some of the most common complexities : $O(1)$, $O(n)$, $O(n^2)$
$O(1)$, $O(n)$, $O(n^2)$ 처럼 빅오가 간단하지 않는 경우가 있다.
Sometimes big O expressions involve more complex mathematical expressions
빅오 표기들 중에 더 어렵거나 덜 흔한 수학 개념들도 포함되어 있을 수 있다.
One that appears more often than you might like is the logrithm
그 중에 자주 나오는 개념이 로그이다.
로그함수
로그함수는 지수함수의 역할이다.
나눗셈과 곱셈이 짝인것처럼 로그함수와 지수합수는 짝이 된다.
$log_2(8) = 3$ → $2^3 = 8$
2를 밑으로 하는 어떤 값의 로그는 어떤 지수값과 같다.
$log_2(value) = e$ → $2^e = value$
We’ll omit the 2.
해당 글에서는 전체적으로 큰 틀에 신경쓰기 때문에 2는 생략하고 그냥 log라고 한다.
$log === log_2$
logarithm Example 📝
* rule of thumb
The logarithm of a number roughly measures the number of times your can divide that number by 2 before your get a value that’s less than or equal to one.
간단한 규칙으로, 어떤 이진 로그를 대략 계산하기 위해서는
그 숫자가 1보다 작아지기 전에 2로 나눠지는 횟수이다.

실제 계산이 중요하지는 않다.
중요한 것은 그래프에서 어떨게 보이는지이다.
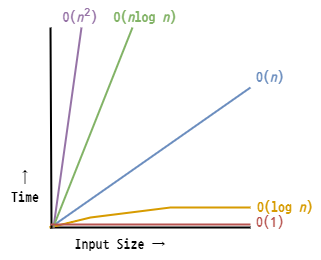
logarithm Complexity 📈
아래의 그래프를 보면 알다시피 로그 시간 복잡도는 아주 좋다.
Big O Time Complexity
로그와 관련있는 것들
-
Certain searching algorithms have logarithmic time complexity.
어떤탐색 알고리즘들은 로그 시간 복잡도를 가지고 있다. -
Efficient sorting alforithms involve logarithms.
효율적인정렬 알고리즘들도 로그와 관련되어 있다. -
Recursion sometimes involves logarithmic space complexity.
재귀(再歸)도 때때로 로그 공간 복잡도를 포함한다.
Big O 알고리즘 총 정리
-
To analyze the performance of an algorithm, we use Big O Notation
알고리즘 성능을 분석하기 위해서 Big O 표기법을 사용한다. -
Big O Notation can give us a high level understanding of the time or space complexity of an algorithm
빅오를 통해서 시간과 공간 복잡도에 대한 이해를 높일 수 있다. -
Big O Notation doesn’t care about precision, only about general trends (lenear? quadratic? constant?)
빅오 표기법은 정확도가 아니라 전체적인 추세를 중요하게 여긴다. -
The time or space complexity (as measured by Big O) depends only on the algorithm, not the hardware used to run the algorithm
빅오로 측정되는 알고리즘의 시간과 공간 복잡도는 하드웨어에 영향을 받지 않는다.
차이가 있을 수 있으나 전반적인 추세는 다르지 않다.
빅오는 실행될 연산의 갯수를 따지기 때문이다.
🌞 정보 : 공부 기록용 블로그입니다. 오타나 내용 오류가 있을 경우 알려주시면 감사하겠습니다.

댓글남기기